Topic 4: Sets with Exercises

What is Sets?

A set is a collection of objects that have something in common or follow a rule. The objects in the set are called its element. Curly braces are used to indicate that the objects written between them belong to a set. Every object in a set is unique. It is not necessary to list every object in the set. Instead, the rule that the objects follow can be given in the braces. We can define a set by listing its elements or by describing its elements. The latter method is useful when working with large sets.

Set Symbols

A set is a collection of things, usually numbers. We can list each element (or "member") of a set inside curly brackets like this:

Notation

There is a fairly simple notation for sets. We simply list each element (or "member") separated by a comma, and then put some curly brackets around the whole thing:

The curly brackets { } are sometimes called "set brackets" or "braces".

This is the notation for the two previous examples:

{socks, shoes, watches, shirts, ...}
{index, middle, ring, pinky}

Notice how the first example has the "..." (three dots together).

The three dots ... are called an ellipsis, and mean "continue on".  

Numerical Sets

So what does this have to do with mathematics? When we define a set, all we have to specify is a common characteristic. Who says we can't do so with numbers?

Set of even numbers: {..., -4, -2, 0, 2, 4, ...}
Set of odd numbers: {..., -3, -1, 1, 3, ...}
Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...}
Positive multiples of 3 that are less than 10: {3, 6, 9}

And the list goes on. We can come up with all different types of sets.
There can also be sets of numbers that have no common property, they are just defined that way. For example:

{2, 3, 6, 828, 3839, 8827}
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203}

Are all sets that I just randomly banged on my keyboard to produce.

Universal Set

		At the start we used the word "things" in quotes. We call this the universal set. It's a set that contains everything. Well, not exactly everything. Everything that is relevant to our question.
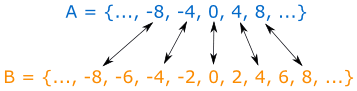
		Then our sets included integers. The universal set for that is all the integers. In fact, when doing Number Theory, this is almost always what the universal set is, as Number Theory is simply the study of integers.

Some More Notation

When talking about sets, it is fairly standard to use Capital Letters to represent the set, and lowercase letters to represent an element in that set. So for example, A is a set, and a is an element in A. Same with B and b, and C and c. Example: Set A is {1,2,3}. We can see that 1 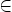 A, but 5  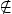A

Equality

Two sets are equal if they have precisely the same members. Now, at first glance they may not seem equal, so we may have to examine them closely!

Example: Are A and B equal where:

• A is the set whose members are the first four positive whole numbers
• B = {4, 2, 1, 3}

Let's check. They both contain 1. They both contain 2. And 3, And 4. And we have checked every element of both sets, so: Yes, they are equal!

And the equals sign (=) is used to show equality, so we write:

A = B

Subsets

When we define a set, if we take pieces of that set, we can form what is called a subset.

Example: the set {1, 2, 3, 4, 5}

A subset of this is {1, 2, 3}. Another subset is {3, 4} or even another is {1}, etc.
But {1, 6} is not a subset, since it has an element (6) which is not in the parent set.

In general:

A is a subset of B if and only if every element of A is in B.

Example: Is A a subset of B, where A = {1, 3, 4} and B = {1, 4, 3, 2}?

1 is in A, and 1 is in B as well. So far so good.
3 is in A and 3 is also in B.
4 is in A, and 4 is in B.
That's all the elements of A, and every single one is in B, so we're done.

Yes, A is a subset of B

Note that 2 is in B, but 2 is not in A. But remember, that doesn't matter, we only look at the elements in A.

Let's try a harder example.

Example: Let A be all multiples of 4 and B be all multiples of 2. Is A a subset of B? And is B a subset of A?

Well, we can't check every element in these sets, because they have an infinite number of elements. So we need to get an idea of what the elements look like in each, and then compare them.
The sets are:

• A = {..., -8, -4, 0, 4, 8, ...}
• B = {..., -8, -6, -4, -2, 0, 2, 4, 6, 8, ...}

By pairing off members of the two sets, we can see that every member of A is also a member of B, but every member of B is not a member of A:

So:

A is a subset of B, but B is not a subset of A

Proper Subsets

So doesn't that mean that A is a subset of A?

This doesn't seem very proper, does it? We want our subsets to be proper. So we introduce (what else but) proper subsets.

A is a proper subset of B if and only if every element in A is also in B, and there exists at least one element in B that is not in A.

This little piece at the end is only there to make sure that A is not a proper subset of itself. Otherwise, a proper subset is exactly the same as a normal subset.

Example:

{1, 2, 3} is a subset of {1, 2, 3}, but is not a proper subset of {1, 2, 3}.

Example:

{1, 2, 3} is a proper subset of {1, 2, 3, 4} because the element 4 is not in the first set.

Notice that if A is a proper subset of B, then it is also a subset of B.

Even More Notation

When we say that A is a subset of B, we write A 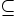 B.
Or we can say that A is not a subset of B by A 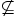 B ("A is not a subset of B")
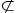When we talk about proper subsets, we take out the line underneath and so it becomes A  B or if we want to say the opposite, A  B.

Empty (or Null) Set

This is probably the weirdest thing about sets.

As an example, think of the set of piano keys on a guitar.

"But wait!" you say, "There are no piano keys on a guitar!"

And right you are. It is a set with no elements.
This is known as the Empty Set (or Null Set).There aren't any elements in it. Not one. Zero.
It is represented by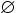 
Or by {} (a set with no elements)
Some other examples of the empty set are the set of countries south of the south pole.
So what's so weird about the empty set? Well, that part comes next.

Empty Set and Subsets

So let's go back to our definition of subsets. We have a set A. We won't define it any more than that, it could be any set. Is the empty set a subset of A?
Going back to our definition of subsets, if every element in the empty set is also in A, then the empty set is a subset of A. But what if we have no elements?
It takes an introduction to logic to understand this, but this statement is one that is "vacuously" or "trivially" true.
A good way to think about it is: we can't find any elements in the empty set that aren't in A, so it must be that all elements in the empty set are in A.
So the answer to the posed question is a resounding yes.

The empty set is a subset of every set, including the empty set itself.

Order

No, not the order of the elements. In sets it does not matter what order the elements are in.

Example: {1,2,3,4} is the same set as {3,1,4,2}

When we say "order" in sets we mean the size of the set.

Just as there are finite and infinite sets, each has finite and infinite order.

For finite sets the order is the number of elements.

Example, {10, 20, 30, 40} has an order of 4.

For infinite sets, all we can say is that the order is infinite. Oddly enough, we can say with sets that some infinities are larger than others, but this is a more advanced topic in sets.

Common Symbols Used in Set Theory

Symbols save time and space when writing. Here are the most common set symbols

In the examples C = {1,2,3,4} and D = {3,4,5}

Symbol	Meaning	Example
{ }	Set: a collection of elements	{1,2,3,4}
A ∪ B	Union: in A or B (or both)	C ∪ D = {1,2,3,4,5}
A ∩ B	Intersection: in both A and B	C ∩ D = {3,4}
A ⊆ B	Subset: A has some (or all) elements of B	{3,4,5} ⊆ D
A ⊂ B	Proper Subset: A has some elements of B	{3,5} ⊂ D
A ⊄ B	Not a Subset: A is not a subset of B	{1,6} ⊄ C
A ⊇ B	Superset: A has same elements as B, or more	{1,2,3} ⊇ {1,2,3}
A ⊃ B	Proper Superset: A has B's elements and more	{1,2,3,4} ⊃ {1,2,3}
A ⊅ B	Not a Superset: A is not a superset of B	{1,2,6} ⊅ {1,9}
Ac	Complement: elements not in A	Dc = {1,2,6,7} When  = {1,2,3,4,5,6,7}
A − B	Difference: in A but not in B	{1,2,3,4} − {3,4} = {1,2}
a ∈ A	Element of: a is in A	3 ∈ {1,2,3,4}
b ∉ A	Not element of: b is not in A	6 ∉ {1,2,3,4}
∅	Empty set= {}	{1,2} ∩ {3,4} = Ø
	Universal set: set of all possible values (in the area of interest)
P(A)	Power Set:  all subsets of A	P({1,2}) = { {}, {1}, {2}, {1,2} }
A = B	Equality: both sets have the same members	{3,4,5} = {3,4,5}
A×B	Cartesian Product: set of ordered pairs from A and B	{1,2} × {3,4} = {(1,3), (1,4), (2,3), (2,4)}
|A|	Cardinality: the number of elements of set A	|{3,4}| = 2
|	Such that	{ n | n > 0 } = {1,2,3,...}
:	Such that	{ n : n > 0 } = {1,2,3,...}
∀	For All	∀x>1, x2>x
∃	There Exists	∃ x | x2>x
∴	Therefore	a=b ∴ b=a
	Natural Numbers	{1,2,3,...} or {0,1,2,3,...}
	Integers	{..., -3, -2, -1, 0, 1, 2, 3, ...}
	Rational Numbers
	Algebraic Numbers
	Real Numbers
	Imaginary Numbers	3i
	Complex Numbers	2 + 5i

Here is the video of sets:

-EXERCISE-

!GOOD LUCK!

Question 1:
A is the set of factors of 12.
Which one of the following is not a member of A?

Question 2: 

X is the set of multiples of 3 
Y is the set of multiples of 6
Z is the set of multiples of 9

Which one of the following is true?

(⊂ means "subset")

Question 3:

A = {a, b, c, d}
How many subsets does the set A have?

Topic 5: Indices with Exercises

What is Probability?
How likely something is to happen.

Definition:
The probability of an event is the measure of the chance that the event will occur as a result of an experiment. The probability of an event A is the number of ways event A can occur divided by the total number of possible outcomes.

Tossing a coin

When  a coin is tossed, there are two possible outcomes:

• Head (H) or
• Tails (T)

We say that the probability of the coin landing H is 1/2.
And the probability of the coin landing T is 1/2.






Throwing a dice

When a single die is thrown, there are six possible outcomes: 1,2,3,4,5,6.

The probability of any one of them is 1/6.



In general probability

Probability of an event happening=Number of ways it can happenTotal number of outcomes

Example: the chances of rolling a "4" with a die

Number of ways it can happen: 1 (there is only 1 face with a "4" on it)

Total number of outcomes: 6 (there are 6 faces altogether)

So the probability = 16

Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble gets picked?

Number of ways it can happen: 4 (there are 4 blues)

Total number of outcomes: 5 (there are 5 marbles in total)

So the probability = 45 = 0.8

Example 1:	A spinner has 4 equal sectors colored yellow, blue, green and red. After spinning the spinner, what is the probability of landing on each color?
Outcomes:	The possible outcomes of this experiment are yellow, blue, green, and red.
Probabilities:	P(yellow)  =  # of ways to land on yellow  =  1 total # of colors  4  P(blue)  =  # of ways to land on blue  =  1 total # of colors  4  P(green)  =  # of ways to land on green  =  1 total # of colors  4  P(red)  =  # of ways to land on red  =  1 total # of colors  4  Example 2:  Choose a number at random from 1 to 5. What is the probability of each outcome? What is the probability that the number chosen is even? What is the probability that the number chosen is odd? Outcomes:   The possible outcomes of this experiment are 1, 2, 3, 4 and 5. Probabilities:   P(1)  =  # of ways to choose a 1  =  1 total # of numbers 5 P(2)  =  # of ways to choose a 2  =  1 total # of numbers 5 P(3)  =  # of ways to choose a 3  =  1 total # of numbers 5 P(4)  =  # of ways to choose a 4  =  1 total # of numbers 5 P(5)  =  # of ways to choose a 5  =  1 total # of numbers 5 P(even)  =  # of ways to choose an even number  =  2 total # of numbers 5 P(odd)  =  # of ways to choose an odd number  =  3 total # of numbers 5 The outcomes 1, 2, 3, 4 and 5 are equally likely to occur as a result of this experiment. However, the events even and odd are not equally likely to occur, since there are 3 odd numbers and only 2 even numbers from 1 to 5. Example 3:   A glass jar contains 6 red, 5 green, 8 blue and 3 yellow marbles. If a single marble is chosen at random from the jar, what is the probability of choosing a red marble? a green marble? a blue marble? a yellow marble? Outcomes:   The possible outcomes of this experiment are red, green, blue and yellow. Probabilities:   P(red)  =  # of ways to choose red  =   6   =   3  total # of marbles 22 11 P(green)  =  # of ways to choose green  =   5  total # of marbles 22 P(blue)  =  # of ways to choose blue  =   8   =   4  total # of marbles 22 11 P(yellow)  =  # of ways to choose yellow  =   3  total # of marbles 22 The outcomes in this experiment are not equally likely to occur. You are more likely to choose a blue marble than any other color. You are least likely to choose a yellow marble. Here are the video of the Probability: -EXERCISE- !GOOD LUCK! Question 1:  A dice is thrown once. What is the probability that the score is a factor 6? a) 1/6 b) 1/2 c) 2/3 d) 1 Question 2: The diagram shows a spinner made up of a piece of card in the shape of a regular pentagon, with a toothpick pushed through its center. The five triangles are numbered from 1 to 5. The spinner is spun until it lands on one of five edges of the pentagon. What is the probability that the number it lands on is odd?  a) 1/5 b) 2/5 c) 1/2 d) 3/5 Question 3: A card is chosen at random from a deck of 52 playing cards. There are 4  Queens and 4 Kings in a deck of playing cards. What is the probability the card chosen is a Queen or  a King? a) 1/13 b) 2/13 c) 1/8 d) 2/11

Topic 9: Sequence and Number Pattern with Exercises

What is Sequence?
A sequence is a list of things (usually numbers) that are in order.

Infinite or Finite

When the sequence goes on forever it is called an infinite sequence,
otherwise it is a finite sequence

Examples:

{1, 2, 3, 4, ...} is a very simple sequence (and it is an infinite sequence)

{20, 25, 30, 35, ...} is also an infinite sequence

{1, 3, 5, 7} is the sequence of the first 4 odd numbers (and is a finite sequence)

{4, 3, 2, 1} is 4 to 1 backwards

{1, 2, 4, 8, 16, 32, ...} is an infinite sequence where every term doubles

{a, b, c, d, e} is the sequence of the first 5 letters alphabetically

{f, r, e, d} is the sequence of letters in the name "fred"

{0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s (yes they are in order, it is an alternating order in this case)

Like a Set

A Sequence is like a Set, except:

• the terms are in order (with Sets the order does not matter)
• the same value can appear many times (only once in Sets)

Example: {0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s.

The set is just {0,1}

Notation

Sequences also use the same notation as sets: list each element, separated by a comma, and then put curly brackets around the whole thing.

{3, 5, 7, ...}

The curly brackets { } are sometimes called "set brackets" or "braces".

A Rule

A Sequence usually has a Rule, which is a way to find the value of each term.

Example: the sequence {3, 5, 7, 9, ...} starts at 3 and jumps 2 every time:

As a Formula

Saying "starts at 3 and jumps 2 every time" is fine, but it doesn't help us calculate the:

• 10^th term,
• 100^th term, or
• n^th term, where n could be any term number we want.

So, we want a formula with "n" in it (where n is any term number).

So, What Can A Rule For {3, 5, 7, 9, ...} Be?

Firstly, we can see the sequence goes up 2 every time, so we can guess that a Rule is something like "2 times n" (where "n" is the term number). Let's test it out:

Test Rule: 2n

n	Term	Test Rule
1	3	2n = 2×1 = 2
2	5	2n = 2×2 = 4
3	7	2n = 2×3 = 6

That nearly worked ... but it is too low by 1 every time, so let us try changing it to:

Test Rule: 2n+1

n	Term	Test Rule
1	3	2n+1 = 2×1 + 1 = 3
2	5	2n+1 = 2×2 + 1 = 5
3	7	2n+1 = 2×3 + 1 = 7

That Works!

So instead of saying "starts at 3 and jumps 2 every time" we write this:

2n+1

Now we can calculate, for example, the 100th term:

2 × 100 + 1 = 201

Many Rules

But mathematics is so powerful we can find more than one Rule that works for any sequence.

Example: the sequence {3, 5, 7, 9, ...}

We have just shown a Rule for {3, 5, 7, 9, ...} is: 2n+1

And so we get: {3, 5, 7, 9, 11, 13, ...}

But can we find another rule?

How about "odd numbers without a 1 in them":

And we get: {3, 5, 7, 9, 23, 25, ...}

A completely different sequence!

And we could find more rules that match {3, 5, 7, 9, ...}. Really we could.

So it is best to say "A Rule" rather then "The Rule" (unless we know it is the right Rule).

Notation

To make it easier to use rules, we often use this special style:

xn is the term n is the term number

Example: to mention the "5th term" we write: x₅

So a rule for {3, 5, 7, 9, ...} can be written as an equation like this:

x_n = 2n+1

And to calculate the 10th term we can write:

x₁₀ = 2n+1 = 2×10+1 = 21

Can you calculate x₅₀ (the 50th term) doing this?

Here is another example:

Example: Calculate the first 4 terms of this sequence:

{a_n} = { (-1/n)ⁿ }

Calculations:

• a₁ = (-1/1)¹ = -1
• a₂ = (-1/2)² = 1/4
• a₃ = (-1/3)³ = -1/27
• a₄ = (-1/4)⁴ = 1/256

Answer:

{a_n} = { -1, 1/4, -1/27, 1/256, ... }

Triangle Number

1, 3, 6, 10, 15, 21, 28, 36, 45, ...

The Triangle Number Sequence is generated from a pattern of dots which form a triangle:

By adding another row of dots and counting all the dots we can find the next number of the sequence.

But it is easier to use this Rule:

x_n = n(n+1)/2

Example:

• the 5th Triangular Number is x₅ = 5(5+1)/2 = 15,
• and the sixth is x₆ = 6(6+1)/2 = 21

Square Numbers

1, 4, 9, 16, 25, 36, 49, 64, 81, ...

The next number is made by squaring where it is in the pattern. 

Rule is x_n = n²

Cube Numbers

1, 8, 27, 64, 125, 216, 343, 512, 729, ...

The next number is made by cubing where it is in the pattern. 

Rule is x_n = n³

-EXERCISE-
!GOOD LUCK!

Question 1:

The first positive square number is squared  1² = 1 × 1 = 1

What is the tenth positive square number?

a) 20

b) 81

c) 100

d) 1 000

Question 2:

2, 3, 5, 8, 12, ...
What is the next number in the above sequence?

a) 16

b) 17

c) 18

d) 20

Question 3:

1, 3, 7, 15, 31, ...
What is the next number in the above sequence?

a) 47

b) 48

c) 62

d) 63